our buggy moral code

Dan Ariely is a professor of psychology and behavioral economics at Duke university, he has posted many videos on-line about topics in behavioral economics, in this particular video he talks about cheating, and in what situations would people cheat more and when would they cheat less. To do this study he did an experiment where he handed out a sheet of paper that had 20 simple math problems and he would give the participants a certain amount of money for every question that they got correctly but the trick was that he only gave them 5 mins; on avg a normal person would solve 4 problems, when he asked the participants to keep the paper that had the questions he found out that now people apparently solved 7 problems, he also found out that people would cheat a little bit. he explained that people cheat a little bit because of something called personal fudge factor and this basically means people cheat just enough as long as it doesn't change out impression of ourselves. Then he asks how do we measure the personal fudge factor, to do this he set up 2 experiments, the first was to decrease the fudge factor, and the second was to increase the fudge facto. in the first experiment he asked people to remember the 10 commandments, but he couldn't do this experiment in college so he asked people to sign an honor code and he found out no one has cheated. in the second experiment he did the same thing with the money experiment but in this one he divided the group into thirds; 1/3 of the people shredded the paper and said i solved x number of problems and the got paid for it, another 1/3 gave back the paper and got paid, another 1/3 shredded the paper then asked the experimenter if they can get paid in tokens then they would take these tokens 12ft over and change the tokens for money he found out that this 1/3 doubled their cheating because they didn't get paid directly. In a third experiment in college he gave the students prepaid envelops and then asked the students to return whatever amount was left; in this experiment they hired an acting student that clearly cheated and got away with it, what he found out was that people increase cheating when they see someone in their group cheat but when they see an outside person they cheated less. at the end he concluded that he found out that people cheat often but by a bit, when they are reminded of their morality they cheat less, and when you increase the distance of money people cheated more.

TED is a site where scholars talk about a single focus in their respective fields for roughly twenty minutes at a time.

This is another video by Dan Ariely. Here Ariely talks about the inevitability of making decisions. Most people believe that they make choices based on their cognitive ability, meaning they actively make decisions based on preference. However, Ariely's talk actually refutes this belief. Ariely, through the use of various studies seen in the video, proves that decisions are influenced by the potential choices. This seems obvious enough, however, Ariely goes on step further in showing that even choices that would never be chosen influence our decisions.

An example used in the video goes as follows: A man's face is placed near another man's face. Then a third face, a slightly distorted, and uglier version of the first man is placed in the line up. Most people would rate the first undistorted man's face as more attractive than his distorted clone, as well as more attractive than the other man. When the same two faces were placed in a line up, but this time with the other man's face distorted, the results showed that he was viewed as more attractive. This is incredibly interesting. When we make decisions we do not completely realize all of the factors that go into these decisions. In many ways we are not in control of our own behavior. In the beginning of his talk Ariely shows several optical illusions, which are designed so that humans view them in a specific, and incorrect way. Behavior works in much the same as an optical illusion. Something in everyday life triggers the way we act, and even if we know the effects of the things, our brain tells us to make the same decisions. This is similar to how we cannot un-see the effects of many optical illusions despite knowing their properties.

This realization is quite depressing. How much control do we have over our everyday decisions? Not very much it seems. However, this is not necessarily bad. If we can learn how people make decisions we can just as easily create scenarios in which they make decisions we want them to make. As in the case Ariely used with the faces, if the man had gone out to a club along with his distorted self, he would be more likely to be viewed more handsome by the opposite sex. So these human quirks are exploitable.

Veiled Intentions

Why do people veil obvious intentions in day to day speech:

RSA Animate is a project to create interesting animated videos out of equally interesting talks about the field of psychology and other such fields. For behavioral economists this video has incredible insight into "the three major human relationships": dominance, communality, and reciprocity. Each of these relationships call for different types of social interaction. The way a person speaks to a boss is quite different from how they speak to a friend.

Innuendos are easier to deal with than direct statements. We are more comfortable with both using them and receiving them. This comfortability comes with the notion that anything that is said outright cannot be taken back. As soon as someone makes a blatant statement it is out there, in the open, and cannot be undone. With a veiled statement, even one that has obvious intentions, there is the feeling that it can be forgotten. The true meaning is not out in the open, and even if the request or notion is rejected then the relationship between the people involved will not be compromised.

As far as practical applications go, we do this sort of thing without even noticing. We modify our behavior to fit the situations we find ourselves in. Foot-in-the-door and door-in-the-face techniques are quite similar. We naturally seek to optimize our chances of successful social interaction. We try to avoid awkwardness and do so by blanketing our statements to reduce possible backlash. We might be better off going around speaking metaphorically and veiling our statements always. But then again, that might make everyday interactions fairly annoying.

Behavioral Game Theory: Experiments in Strategic Interaction by Colin F. Camerer

This is an essay about the book  Behavioral Game Theory: Experiments in Strategic Interaction by Colin F. Camerer. The book is about Behavioral game theory which is a branch of behavioral economics. Game theory is when people, genes, or nations interact. Acoording to the article game theory is "game theory is a mathematical derivation of what players with different cognitive capabilities are likely to do in games"
  Behavioral Game Theory

What is Behavioral Economics?

This is a video with Dan Ariely the author of Predictably Irrational. It talks about the difference between behavioral economics and standard economics. It says that standard economics has more to do with formulas and algorithms, and behavioral economics has experiments that tell us what we can do and what we can’t do, how people actually make decisions, what we are good at and when are actually being irrational.

Is Tit for Tat a Viable Strategy?

Bit of a long one, but here it is:

Tit for tat, as discussed here, is a strategy used for zero-sum games, such as the Prisoner's Dilemma, in game theory. For those who do not know what the Prisoner's Dilemma is, here is a brief explanation:

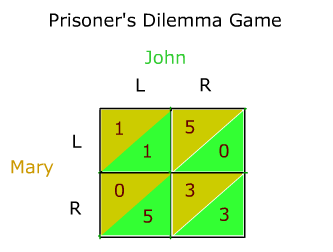
Pictured above is a payoff matrix for the prisoner's dilemma. This particular matrix names the participants John and Mary. The game goes as follows, both John and Mary, who have committed a crime and have been arrested by the police, are given a choice. They can either, remain silent or tell the police that the other person committed the crime. If one player remains silent, while the other blames then the one who remained silent will face five years in jail. If both players blame the each other, then they are each given a three year sentence. And lastly, if both players remain silent, they are both sentenced to only one month in jail. The chart above can be read quite easily if it is understood that 'L' means to remain silent (or cooperate), and 'R' means to blame the other (or defect).

Though the Prisoner's Dilemma is often only played one time, it is possible to adapt it so that there are multiple trials. In Professor Maynard's Psychology 272 class such a game was played. In groups of two, players employed various strategies in a ten round zero sum game. Of these strategies was tit for tat, a strategy which starts with the player cooperating with the opponent, and then following the opponent's lead (if the opponent defects, then the player defects. If they cooperate, then the player cooperates). After, the results of the games were tallied. They showed that tit for tat seemed to generate the highest combined score in the class. But the question is: do these statistics indicate that tit for tat is a good behavioral strategy? More specifically, if both players play their strategy perfectly does tit for tat really win most of the time?

Most people will answer that tit for tat is a viable strategy, however let us examine several different scenarios. Terms to know: Cooperative - a strategy that for the most part entails cooperating with the opponent, and defecting seldom. Defective - a strategy that, for the most part, entails defecting with little cooperation.
1. Tit for tat versus Cooperative: If both players execute their strategies correctly, the game should result in the positive payoff for both players. Meaning both players cooperate at every turn. However, it is actually possible for the cooperative player to get a higher score than the tit for tat player, if at the last turn the cooperative player defects. If this happens, then the Tit for tat player, who by his own strategy is forced to cooperate, will have a lower score. Thus, in a two player zero-sum game it seems that cooperative strategy works well against tit for tat.

2. Tit for tat versus Defective: If both players execute their strategies correctly in this case, the game should result in the defective player always having a higher score than the Tit for tat player. This occurs because the Tit for tat player will always start as cooperative, and so the defective player's defect in the very first round of the game will give him the advantage. Following the first round both players should proceed to defect for the remainder of the game. This will always result in the defective player's victory over the tit for tat player. Even if the defective player does not defect on the very first term, he only needs to make sure that once he defects that he continues to defect. This will ensure a higher score than the Tit for tat player.

3. Tit for tat versus tit for tat: If both players execute their strategy correctly in this case, the game should result in both having the same score. The two players will merely cooperate until the game has ended.

In exploring the way tit for tat works against itself and two basic strategies of game theory, it is still hard to understand why tit for tat is considered a good strategy. Richard Dawkins discusses its merits:

Tit for tat excels in the long run, despite the fact that it can never actually get a higher score against a single opponent. Games that involve tit for tat, on average generate higher scores which, in the long run, make tit for tat seem like the most viable strategy.

Practically speaking, tit for tat is a good strategy to employ if a person is willing to take a backseat to their fellow player. In the long run the tit for tat player will benefit the most, but in each isolated incident the tit for tat player will not seem to come out on top. These results express that in most job situations, where employees are competing for a raise, it is more likely that a worker who uses a tit for tat strategy while working with fellow co-workers will have a far more impressive work history than those who are more ego-minded. Tit for tat excels when it meets other cooperative strategies, but is not so agreeable that it is taken advantage of by defective ones.

I also found that this picture was a good example of behavioral economics. It shows how, even though the hat is way too big for the man purchasing it, he gets the large anyway because the savings is higher, making him feel like the purchase was more worth it even though every other hat is the same exact price. The bigger the sale, the more likely someone will buy it, even if it isn't exactly what they are looking for. They feel like they are saving so much money even though they would be spending the same amount of money in the end.